QUANTIQUE (ÉLECTRODYNAMIQUE)

QUANTIQUE (ÉLECTRODYNAMIQUE)

L’électrodynamique quantique est une théorie qui décrit les interactions entre le champ électromagnétique quantifié et les particules avec charge électrique. C’est un exemple d’une théorie relativiste quantique des champs où le champ – dans ce cas, le champ électromagnétique de Maxwell, médiateur des interactions entre particules chargées – est aussi quantifié, c’est-à-dire conçu en termes de particules, les quanta du champ, qu’on appelle des photons. La validité de l’électrodynamique quantique a pu être testée avec une précision remarquable (moins d’une partie par million dans certains cas), grâce au fait qu’il existe dans la nature des particules pour lesquelles l’interaction dominante est due à la charge électrique (c’est le cas des leptons chargés, dont l’électron et le positron sont les exemples les mieux connus). Dans ce sens, la théorie est un succès du concept de «quantification», appliqué au cas d’un système relativiste à nombre infini de degrés de liberté.

L’électrodynamique quantique est aussi l’exemple le plus simple d’une théorie quantique des champs de jauge: elle est invariante par rapport à un ensemble de transformations locales opérant sur les champs, champ électromagnétique et champ de matière; ces opérations forment un groupe abélien appelé le groupe de jauge U(1) (cf. SY- MÉTRIE [physique]). C’est justement la généralisation de cette propriété d’invariance de jauge, à des groupes non abéliens associés à d’autres charges, qui a été exploitée pour formuler des théories quantiques de champs susceptibles de décrire d’autres interactions fondamentales: les interactions faibles, responsables par exemple de la radioactivité 廓, et les interactions fortes qui gouvernent les forces nucléaires ^{[cf. PARTICULES ÉLÉMENTAIRES]}.

1. Description de la théorie

Les équations de l’électrodynamique classique (cf. ÉLECTRICITÉ - Électromagnétisme) sont les équations de Maxwell. Dans leur formulation covariante ^{[cf. RELATIVITÉ]}, elles s’écrivent:

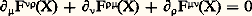et: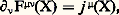

où j 猪(X) est la source de densité de courant électromagnétique; j⁰ (X), la densité de charge; ゃ(X), la densité de courant électrique.

Le symbole 煉 size=1^猪 令 煉/ 煉X size=1^猪 dénote la dérivation par rapport au quadrivecteur espace-temps X 猪 (X⁰ est la composante temps, X¹,²,³ les composantes d’espace). Une somme sur les indices répétés est sous-entendue; F 猪益(X) est le tenseur champ électromagnétique (F size=1^猪益 = 漣 F size=1^益猪) qui a pour composantes le champ électrique:

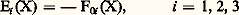et le champ magnétique:

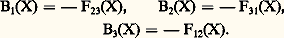La première équation est automatiquement satisfaite lorsque F size=1^猪益(X) est exprimé en fonction du champ quadrivecteur potentiel A size=1^猪(X):

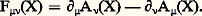Réciproquement, la première équation implique l’existence d’un potentiel A 猪(X) défini modulo le gradient d’un champ scalaire 淋(X) arbitraire. La transformation:

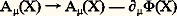est appelée une transformation de jauge et l’invariance des équations de Maxwell par rapport à cette transformation, l’invariance de jauge .

La description de l’interaction d’une particule chargée de spin 1/2 ^{[cf. SPIN]} tel l’électron avec le champ électromagnétique se fait à l’aide d’un champ spinoriel 切(X), le champ de Dirac ^{[cf. DIRAC (P.)]}. Cette description est invariante par rapport aux changements de phase du champ 切(X), c’est-à-dire par rapport aux transformations:

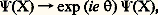où e désigne l’unité de charge électrique et un nombre réel arbitraire. La conséquence physique de cette invariance, qu’on appelle invariance de jauge de première espèce , ou encore invariance de jauge globale ( est indépendant du point d’espace-temps X) est la conservation de la charge électrique .

L’invariance des lois physiques par rapport aux changements locaux de la phase de 切(X) est appelée invariance de jauge locale ou invariance de jauge de deuxième espèce . La transformation correspondante:

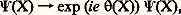où (X) est maintenant une fonction scalaire du même point d’espace-temps que 切(X), laisse les observables physiques invariantes pourvu qu’on transforme simultanément le quadrivecteur potentiel A 猪(X) en:

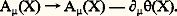Cette invariance locale est à la base d’un type de couplage spécifique entre le champ électromagnétique et le champ de matière: le couplage minimal radiation-matière, généralisation de la loi d’Ampère , qui décrit l’interaction du champ potentiel A 猪(X) avec le courant électromagnétique engendré par les sources de matière.

La dynamique d’une théorie des champs est spécifiée lorsqu’on se donne la fonction densité de Lagrange (lagrangien) correspondante. Dans le cas de l’électrodynamique, cette densité a une forme remarquablement simple:

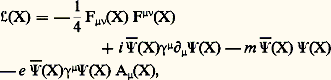切 漣(X) étant le champ spinoriel adjoint. Le symbole 塚猪 représente, ici, quatre matrices de dimensions 4 憐 4, les matrices de Dirac associées à la description des particules et antiparticules de spin 1/2. Ces matrices agissent dans un espace à quatre composantes où le champ spinoriel 切(X) est défini. Cette complexité spinorielle n’est qu’apparente. En fait, elle permet une description tout à fait symétrique du champ de matière (l’électron, par exemple) et du champ d’antimatière correspondant (le positron, dans ce cas). Les paramètres de la théorie sont la masse m de la particule et la charge électrique e . Le premier terme du lagrangien décrit la dynamique associée à la radiation électromagnétique pure. Les deuxième et troisième termes décrivent la dynamique des particules de spin 1/2 avec masse m , sans interaction. Le dernier terme est le couplage minimal d’interaction matière-radiation. Lorsqu’on quantifie les champs libres de matière 切(X) et de radiation A 猪(X) et que l’on traite le terme d’interaction dans le lagrangien comme une perturbation du système libre, il est possible de résoudre les équations du mouvement issues du lagrangien par une méthode d’approximations successives, sous forme d’une série formelle en puissances de la constante du couplage matière-radiation, c’est-à-dire de la charge électrique e . Ce sont les seules solutions de l’électrodynamique quantique que nous connaissions à l’heure actuelle. En fait, la quantité qui apparaît de façon naturelle dans cette série perturbative est, en réalité, la constante de structure fine 見, nombre sans dimensions, défini par la relation:

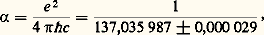où 寮 = h /2 神, h étant la constante de Planck et c la vitesse de la lumière. La valeur expérimentale de 見 size=1^漣1 est celle de E. R. Cohen et B. N. Taylor (1973). (Le système d’unités normalement utilisé en électrodynamique quantique est celui où 寮 = c = 1.) C’est justement le fait empirique que la valeur de 見 est petite (par rapport à l’unité) qui est à l’origine du succès quantitatif de la méthode perturbative.

Une description très pratique de la contribution des différents termes de la série perturbative à un processus donné est celle qu’a introduite R. P. Feynman en 1949, sous forme de diagrammes. Considérons, à titre d’exemple, l’évolution d’un électron soumis à un champ magnétique, le champ magnétique étant ici une source externe non quantifiée. Au niveau du champ libre, le diagramme 1 a représente un électron en interaction avec la source externe. La première perturbation, montrée dans le diagramme 1 b, est celle où l’électron émet et réabsorbe un quanta de radiation du champ électromagnétique, ce qu’on appelle un photon «virtuel». Ce diagramme fait intervenir deux fois le «vertex» fondamental:

associé au terme d’interaction du lagrangien (le terme 漣 e 切 漣 塚 size=1^猪 切A size=1^猪). L’effet, par rapport à celui que décrit le diagramme 1 a, sera donc en e² , c’est-à-dire de l’ordre de 見. Les diagrammes 1 c, d, e de Feynman sont des exemples de contributions à l’ordre 見².

Une grosse difficulté dans la formulation cohérente de la théorie perturbative de l’électrodynamique quantique fut celle qui est liée aux divergences ultraviolettes. Le calcul de diagrammes où apparaissent des boucles (par exemple les diagrammes 1 b, c, d, e) implique des intégrations sur toutes les fréquences possibles des quanta virtuels. Dans la plupart des cas, ces intégrales se révèlent être divergentes dans la région des grandes fréquences (catastrophe ultraviolette). La méthode dite de renormalisation vint à bout de cette difficulté. Trouvant son origine dans les travaux de Feynman, J. Schwinger, S. Tomonaga et F. J. Dyson, des années 1946 à 1953, elle consiste à prouver que toutes les divergences de la théorie peuvent être absorbées dans un choix convenable des champs 切(X) et A 猪(X) et des paramètres masse et charge électrique. L’invariance des observables physiques relativement à ce choix fut remarquée pour la première fois par E. C. G. Stueckelberg et A. Peterman (1953) et indépendamment par M. Gell-Mann et F. E. Low (1954). Cette invariance, qu’on appelle maintenant «invariance par le groupe de renormalisation », a pu fournir une technique puissante en ce qui concerne l’étude du comportement à courtes distances (grandes énergies) de toute théorie quantique des champs qui soit renormalisable ^{[cf. PARTICULES ÉLÉMENTAIRES]}.

2. Les tests de la théorie

Il existe deux types de tests possibles de l’électrodynamique quantique: soit des expériences de diffusion avec des électrons et des photons à hautes énergies, soit des mesures de grande précision de phénomènes électromagnétiques fondamentaux, comme le déplacement de certains niveaux d’énergie dans l’atome d’hydrogène ou le moment magnétique anormal de l’électron et du muon. Dans le premier type d’expérience, on teste de façon spécifique la validité de la théorie à de courtes distances. Lorsque, dans une expérience d’anneaux de collision entre électron (e size=1^漣) et positron (e ⁺), on étudie par exemple la diffusion élastique e ⁺e size=1^漣e ⁺e size=1^漣 et que l’on compare la section efficace observée à celle que prédit la théorie (cf. diagrammes 2 a, b), il est possible de chiffrer la validité de la théorie. Les limites de validité dépendent des impulsions maximales atteintes par les particules virtuelles du processus (dans ce cas, le photon). Par les relations d’incertitude de Heisenberg (cf. mécanique QUANTIQUE), on peut les exprimer sous forme de distances d’interaction de plus en plus petites au fur et à mesure que l’énergie totale du processus augmente. C’est ainsi qu’on a vérifié la validité de l’électrodynamique quantique à des distances d’interaction qui atteignent 5 憐 10 size=1^漣16 cm.

3. Tests de grande précision dans les états liés

Du point de vue historique, c’est le déplacement des niveaux d’énergie 2S^1/2 漣 2P^1/2 dans l’atome d’hydrogène ^{[cf. ATOME]}, mesuré pour la première fois par W. E. Lamb et R. C. Retherford en 1947, qui est à l’origine du développement de l’électrodynamique quantique. Dans la théorie de Dirac de l’atome d’hydrogène, ces deux niveaux sont dégénérés; or, expérimentalement, une mesure précise effectuée, en 1975, par S. R. Lunden et F. M. Pipkin donne une séparation:

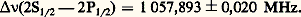L’électrodynamique quantique explique ce déplacement de niveaux par l’interaction de l’électron avec le champ électromagnétique quantifié. La contribution dominante est donnée par les diagrammes 3 a, b de Feynman. L’effet physique du diagramme 3 a est, d’une part, de distribuer la charge ponctuelle de l’électron au sein d’un nuage de charge, d’autre part, de conférer à l’électron un moment magnétique anormal. Le premier phénomène diminue l’effet de liaison coulombienne entre l’électron et le proton, le second phénomène induit une interaction de type magnétique entre l’électron et le proton. En bilan, le niveau 2S est déplacé vers le haut de l’ordre de 1 080 MHz par rapport à celui qui est prédit par la théorie de Dirac.

Le potentiel effectif vu par l’électron est aussi modifié par l’émission d’une paire virtuelle électron-positron (effet de polarisation du vide ) illustré par le diagramme 3 b. Cette polarisation du vide conduit à un effet d’écran qui renforce le potentiel coulombien et, par conséquent, le niveau 2S est déplacé vers le bas de l’ordre de 27 MHz par rapport au niveau prédit par la théorie de Dirac. Un calcul théorique du déplacement de Lamb, tenant compte de beaucoup d’autres effets, donne le résultat suivant (P. J. Mohr, 1975):

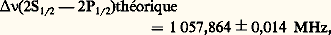en accord avec le résultat expérimental cité plus haut.

Outre le déplacement de Lamb, il y a, aussi, beaucoup de mesures d’autres déplacements de niveaux dans des états liés que l’on a comparés avec les prédictions de l’électrodynamique quantique. À ce sujet, l’étude de la structure hyperfine du niveau fondamental de l’atome d’hydrogène et des systèmes positronium (un atome électron-positron) et muonium (un atome électron-muon positif) est particulièrement intéressante. Dans le cas de l’atome d’hydrogène, la mesure de la structure hyperfine du niveau fondamental (R. Vessot et al., 1966) reste encore le nombre le plus précis jamais obtenu dans une expérience:

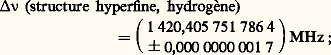ce qui correspond à une précision de 1,2 partie par mille milliards! Cette mesure est sensible à des effets, dus en particulier aux interactions fortes du proton ^{[cf. PARTICULES ÉLÉMENTAIRES]}, que les théoriciens n’ont pas encore été capables de maîtriser à l’heure actuelle.

4. Le moment magnétique anormal de l’électron et du muon

La théorie de Dirac pour une particule de spin 1/2 et de masse m implique un moment magnétique pour cette particule égal à:

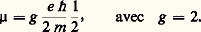L’électrodynamique quantique prédit une déviation de la valeur g = 2 due à des corrections radiatives comme celles qui sont décrites par les diagrammes 1 b, c, d, e de Feynman. On appelle anomalie la quantité:

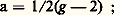c’est une grandeur sans dimensions qui, pour l’électron et le muon, a été mesurée avec une précision remarquable. La mesure de l’anomalie du muon a été obtenue dans une suite de très belles expériences réalisées au C.E.R.N. Le principe expérimental (pour plus de détails et l’historique de ces expériences, voir l’article de F. Farley et E. Picasso cité dans la bibliographie) consiste à mesurer la précession du spin relative à son impulsion en présence d’un champ magnétique homogène (cf. Description relativiste du spin , in chap. 6 de SPIN). Dans le cas du muon, cette mesure est possible grâce à la non-conservation de la parité dans sa désintégration:

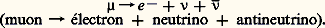La direction de l’électron émis par le muon est en rapport avec le spin du muon (cf. Parité , in chap. 3 de SYMÉTRIE). La dernière expérience faite au C.E.R.N. (1975-1979) a donné le résultat suivant:

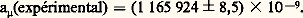Cela est à comparer avec le résultat théorique (cf. J. Calmet, S. Narison, M. Perrottet et E. de Rafael, 1977):

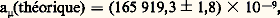résultat qui tient compte des calculs de nombreux théoriciens à l’ordre 見, 見², 見³, des estimations de la contribution des termes d’ordre 見⁴ et des effets dus aux interactions fortes (70,3 size=1^梁 1,7) 憐 10 size=1^漣9 et aux interactions faibles (1,9 size=1^梁 0,1) 憐 10 size=1^漣9. L’erreur due à la valeur de la constante de structure fine est de size=1^梁 0,2 憐 10 size=1^漣9.

Une technique développée par des expérimentateurs de l’université de Washington à Seattle (cf. R. S. Van Dyck, P. B. Schwinberg et H. G. Dehmelt, 1977), dans laquelle un électron est isolé dans une cavité, a permis une mesure de l’anomalie de l’électron qui donne la valeur:

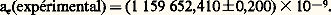Ce résultat est plus précis que la prédiction théorique (cf. Kinoshita T., 1978):

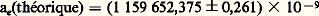qui tient compte des contributions d’ordre 見 (J. Schwinger, 1948), d’ordre 見² (A. Peterman, 1957) et d’ordre 見³ (H. J. Levine et R. Roskies, 1976; R. Barbieri et E. Remiddi, 1975; P. Cvitanovic et Kinoshita T., 1974). Le moment magnétique anormal de l’électron reste aujourd’hui le système qui permet d’avoir le test le plus précis de l’électrodynamique quantique.

Encyclopédie Universelle. 2012.